꿀벌( Apis mellifera  L.)은 여러 생태계의 필수적인 부분입니다 .1 , 생물다양성을 유지하고 2  , 농업 생산성을 증가시킵니다 .3 , 이는 주로 수분 작용에 기여하기 때문입니다 .4 . 일반적인 꿀벌 군집은 수만 마리의 개체로 구성되어 있으며, 이들은 고도로 조직적이고 효율적인 단위로 기능합니다 .5 , 군집 조절의 여러 측면은 구성원들의 집단 행동에서 비롯됩니다 .6 , 7 , 8. 꿀벌 군집의 모든 구성원 중에서 여왕벌이라는 핵심 개체는 군집의 응집력, 성장, 그리고 번식을 유지하는 데 중요한 역할을 합니다 .9 .

이는 군집의 성장과 번식에 대한 책임을 여왕벌에게만 집중시킵니다. 효율성을 극대화하기 위해 여왕벌은 일벌 개체군이 최적의 크기에 도달하도록 탐사와 착취의 균형을 신중하게 맞춰야 합니다. 현재 전략을 개선하는 것(착취)과 새로운 기회를 발견하는 것(탐사) 중 하나를 선택해야 하는 이러한 필요성은 생물학에서 고전적인 상충 관계, 즉 탐사-착취 딜레마를 나타냅니다. 여왕벌이 매일 수천 개의 알을 낳는 능력은 필수 영양소의 가용성, 비어 있지만 준비된 셀의 존재, 그리고 벌집 내에서 이러한 셀을 찾는 능력 등 여러 요인에 달려 있습니다. 여왕벌은 "착취적인" 움직임 패턴을 보여 공간적으로 좁은 공간에 알을 낳고, 산란 효율을 극대화하며 군집의 에너지 관리에 기여할 수 있습니다. 유충 세포는 벌집 전체에 균일하게 분포되지 않고 벌집 중앙에 밀집되어 "유충 둥지"를 형성합니다. 벌통 내 육아실 영역은 벌집의 양면에 위치할 수도 있고, 더 큰 벌통에서는 여러 개의 벌집에 걸쳐 있을 수도 있는데, 이 벌집들은 종종 직접 연결되지 않아 여왕벌이 벌집 사이를 이동해야 합니다. 꿀벌 육아실 발달에는 상당한 에너지와 정확하게 제어된 열 조건이 필요하기 때문에 10 , 육아실 영역 바깥쪽 가장자리 주변의 단열 셀과 함께 촘촘하게 밀집된 벌집은 11  난방 효율에 이점을 제공합니다. 또한, 육아실의 밀도가 높기 때문에 여왕벌이 산란 장소 사이를 이동하는 거리가 최소화됩니다. 반면, 여왕벌은 "탐험" 행동을 보이는데, 일벌이 산란을 위해 갓 준비한 빈 벌집들을 찾기 위해 벌집을 활발하게 탐색하고, 주요 군집 행동을 조절하는 페로몬을 분산시킵니다 12. 요약하자면, 여왕벌은 적절한 산란 장소를 찾기 위한 탐색과 페로몬 분산, 그리고 육아실 영역을 활용하여 산란 효율을 극대화해야 합니다.

산란 전에 여왕은 머리를 그쪽으로 기울여 세포의 적합성을 평가합니다. 적합한 세포를 찾으면 약간 앞으로 나아가 복부를 세포에 넣고 알을 낳습니다. 몇 초 동안 지속되는 이 과정은 여왕의 움직임을 순간적으로 방해하여 움직임이 잠시 멈추게 합니다. 많은 연구에서 모델링 접근법을 통해 새끼 둥지의 출현을 탐구했습니다  13 , 14 , 15 , 16 . 이러한 모델에서 여왕의 이동 행동은 단순히 무작위 걷기로 가정합니다. 여왕의 움직임을 이해하면 꿀벌 군집의 내부 작동 방식을 밝히고 진행 중인 과학적 논쟁에 정보를 제공할 수 있습니다. 움직임의 측면은 시간이 지남에 따라 새끼 둥지 영역과 같은 구조의 형성에 영향을 미치기 때문입니다.

여왕벌의 산란 행동은 적합한 방을 찾는 것을 포함하므로, 곤충의 탐색 행동에서 전형적인 특성을 발견할 것으로 예상합니다. 탐색 행동은 동물이 감지하는 감각 입력, 내재적 동기, 그리고 외부 환경 요인에 따라 달라집니다 .17 꿀벌의 경우, 이러한 외부 요인으로는 벌집의 배치, 기하학적 구조, 중력, 벌집의 온도 기울기, 또는 다른 벌과의 상호작용 등이 있습니다. 관련 연구들은 의사 결정 과정이 환경적 요인이나 내부 요인의 영향을 받는 이동 패턴에 반영될 수 있음을 보여주었습니다 .18 따라서 각 영역 간의 단기 이동 특성 차이를 발견하면 동물의 의사 결정 과정에 대한 더 깊은 이해를 얻을 수 있을 것입니다. 동물의 이동 행동은 일주기 리듬과 같은 내생적 순환에도 상당한 영향을 받을 수 있습니다 .19 만약 이러한 시간적 패턴이 두드러진다면, 이러한 역학을 종종 무시하는 무작위 보행과 같은 단순한 모델은 관찰된 행동의 완전한 복잡성을 포착하기에 충분하지 않을 것입니다. 본 연구에서 우리는 몇 가지 질문을 제기했습니다. 우리는 여왕벌의 움직임에서 각 벌통 영역, 즉 새끼 둥지와 저장(비생식 둥지) 영역 간의 탐색-활용 상충관계가 뚜렷하게 나타나는지 조사하고자 했습니다. 여왕벌의 군집 성장 최적화 전략을 반영하여, 산란 활동이 집중되는 새끼 둥지 영역에서의 움직임은 저장 영역에서의 움직임과 달라야 합니다. 또한, 꿀벌 여왕벌의 거시적 움직임 패턴이 미시적 움직임 패턴에서 도출될 수 있는지, 그리고 이를 통해 미시적 측정값을 거시적 결과와 연결할 수 있는지 확인하고자 합니다.

To systematically investigate these questions, we used methods adopted from the field of movement ecology20, which aims to understand the factors and mechanisms that influence the movement patterns of living organisms. Such movement patterns have been extensively studied in larger animals such as birds21, marine predators22, and mammals23, providing valuable insights into animal ecology24 and the decision-making processes25, the evolutionary aspects26, or the impact of human activities on habitat use27,28. The development of modern tracking technology, like radar tracking29, GPS30 or eDNA31, allowed for great advances in the field, but brings new questions as well32. From trajectory data, descriptive models have been constructed, which model key characteristics of the animals’ movement behavior33,34. These models describe the trajectory polylines as trails of a random walk process; in some cases, this seems to be an emergent property35, in others, there is evidence that the generative process itself is the respective random walk36. Models built on random walk theory were used to describe, for example, the motion of higher-order vertebrates like birds37, jackals38 even humans39 as well as marine predators40, mussels41 and insects like fruitflies42, butterflies43, honeybees44 or ants45.

We present a study of a 22-day long-term dataset we collected using a marker-based visual tracking system of three queens in their hives, with over 34,000 tracklets of the queen trajectory. These tracklets provide us with short-term observations of the movement behavior of an individual. Previous work on insect trajectories worked with much longer segments, e.g., hundreds of meters29, but these works tracked animals in open environments. In contrast, our work focuses on an animal in the confined space of the hive, where the longest possible motion on a straight line would be 47 cm long. Therefore, our observations are representative for the scale of the animal movement.

We investigate fundamental properties of the queen’s behavior, analyzing activity levels and their spatial dynamics. To distinguish between intrinsic movement decisions and extrinsic influences on queen movement, we further fit common random walk models to the empirical tracking data and use simulation to measure their ensemble properties. To investigate the queen’s movement patterns, we employed metrics such as diffusivity, coverage, and first-passage time to measure the explorative aspects of the queen’s motion patterns, and metrics like self-crossing rates and fractal dimension as a measurement of the explorative features of the queens’ motions patterns. We applied these metrics to both empirical trajectories and those generated by our simulations to identify the model that best replicates the observed spatial dynamics. This comparative analysis serves two purposes. It allows us to determine whether a particular model can accurately describe the queen’s movement, and it allows us to draw conclusions on the properties of the movement.

Fig. 1

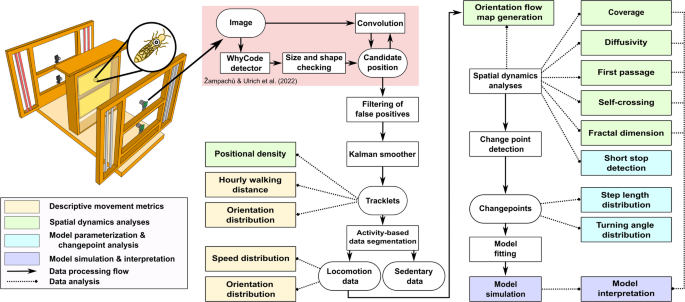
Workflow of Queen Bee Movement Analysis. Upper left illustration: The observation hive, positioned between two panes of glass, was monitored by four cameras that captured all activity across two honeycombs (the lighting setup is illustrational, see Supplementary Methods 1: “Dataset Collection and Processing” for details). Data analysis begins with the WhyComb detector system identifying the tagged queen in the images, followed by size and shape verification to generate candidate positions. These positions undergo convolutional network verification, which leads to candidate refinement by filtering out false positives and generating validated tracklets. A Kalman smoother refines these tracklets for descriptive movement analysis, which includes positional density and hourly walking distance. The data is then segmented into mobile and stationary phases, with the former analyzed for velocity and orientation distributions. Spatial dynamics, including orientation flow map, coverage, diffusivity, first-passage, self-crossing, and fractal dimension, are computed along with short-stop detection. Change point detection facilitates the analysis of step length and turning angle distributions, upon which models are fitted for simulation and comparison with empirical spatial dynamics data.

Full size image

Figure 1 depicts the workflow of the full data analysis approach, showing the processes from data collection, data refinement, descriptive motion analysis, and spatial dynamics analysis up to model simulation and interpretation. Our observation spans three honeybee colonies over a period of 22 days (from August 25, 2022 to September 15, 2022, totaling 528 hours), which covers a whole brood cycle of worker bees (21 days). To the best of our knowledge, no dataset of this extent focusing on the movement of a honeybee queen has been previously published.

Animals observed in this study

This study used three honeybee colonies (Apis mellifera carnica, Pollmann) housed in three standard observation hives, each containing two combs. It is an observational study in its entirety. The bees were allowed to leave the hive ad libitum and forage in the surrounding environment, with each observation hive containing approximately 3,000 to 5,000 individual bees. There were no specific criteria for inclusion or exclusion of honeybee colonies or honeybee queens in this study.

The colonies were commercially bred by the Styrian Beekeeping Center in Graz, Austria, and maintained by professional beekeepers at the University of Graz. The management of the colonies followed strict animal welfare guidelines in accordance with the Austrian Animal Experiments Act (TVG 2012, 1. Abs., §1) and the standards of the Ethics Committee of the University of Graz.